16 Inheritance¶
In OOP this represents the process by which one class inherits (i.e., extends) the properties and methods of another class. It is intended to help reuse existing code with little or no modification, and it is based on hierarchical classifications.
16.1 Hierarchical classification¶
This is a system of grouping things according to a hierarchy or levels of orders. Depending on the application domain considered, such hierarchical classifications will be based on sspecific criteria. In programming, this is something that you have to figure out on your own; more often than not, there is more than just one way you can think about hierarchies. E.g., take a set of people for example. You can classify them as 'tall' or 'short', so you're implicitly thinking of 'height' as being an attribute of the elements of this set (of people). You can also classify them according to 'young' or 'old', in which case you are implicitly considering 'age' as an attribute. There are many other attributes that you can consider in this context.
Some examples of hierarchical classifications are included below to give you an idea of how they work.

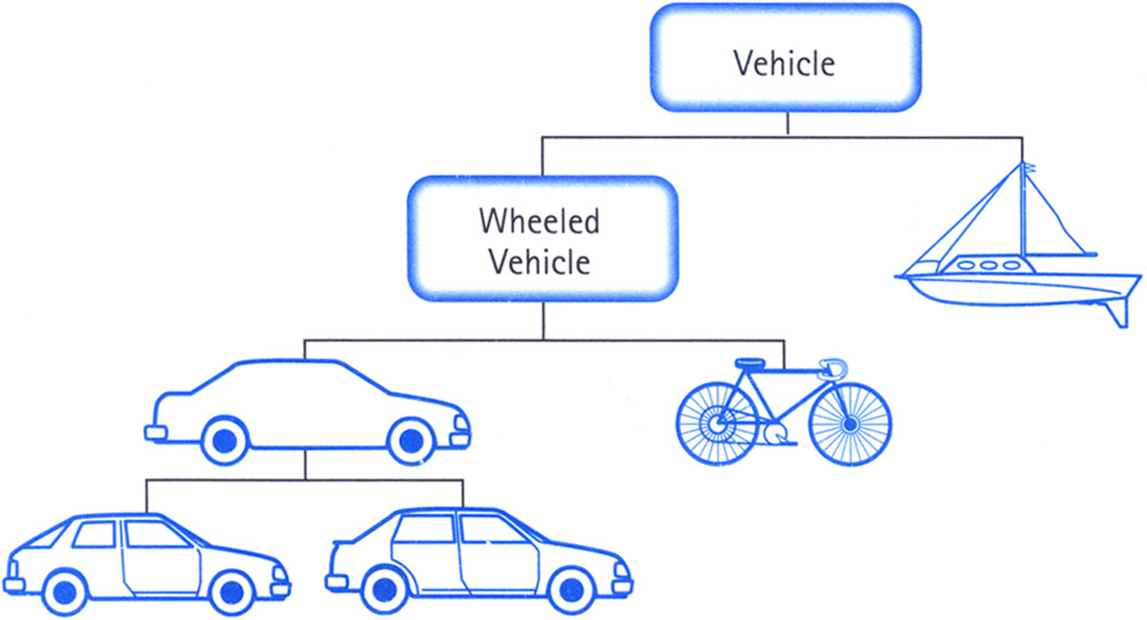

16.2 Terminology¶
Class inheritance is designed to model relationships of the type "$x$ is a $y$" (e.g., a triangle is a shape).

superclass = parent class OR base class
subclass = child class OR derived class
16.3 Types of inheritance¶



16.4 Implementation details¶
This section shows by way of several examples how you can implement basic inheritance in Python (you should keep in mind that this is just an introduction, so much is left out).
First, let's start with a basic implementation of the relationship "a rectangle is a kind of shape".


# a modified version of the code as shown in the above picture:
# the code in the above pictures is Python 2.x (so the syntax looks a bit different,
# below is Python 3.x -- the one we currently use)
class Shape(object):
def __init__(self, col='white'):
self.color = col # col must be a string for the colour
class Rectangle(Shape):
def __init__(self, w, h):
Shape.__init__(self)
self.width = w # width, height = attributes
self.height = h
def area(self):
return self.width*self.height
def set_color(self, col): # this won't be available to the superclass
self.color = col
return
def main():
r1 = Rectangle(10, 5) # instance of the subclass
print('Width for r1: ', r1.width)
print('Height for r1: ', r1.height)
print('\nArea for rectangle: ', r1.area())
print('\n\nDefault colour: ', r1.color)
# change color:
r1.set_color('yellow')
print('New colour: ', r1.color)
main()
Here's another example of inheritance:
# SUPERCLASS:
class Animal(object):
def __init__(self, name):
self.name = name
def eat(self, food):
print('%s is eating %s.' %(self.name, food))
# --------- SUBCLASSES ---------------------------------------
class Dog(Animal):
def fetch(self, thing):
print('%s goes after the %s' %(self.name, thing))
#
#
class Cat(Animal):
def shred(self):
print('%s shreds the string!' %(self.name))
# try out the above subclasses:
def main():
d = Dog('Rodger')
c = Cat('Fluffy')
d.fetch('ball')
c.shred()
# all classes inherited from 'Animal' have a method 'eat()':
d.eat('dog food')
c.eat('cat food')
# note what happens if you try to use the method 'shred()' with
# the wrong type of object:
d.shred()
main()
16.5 Polymorphism¶
Let's start with an example:
# A first example of polymorphism:
class Animal(object):
def __init__(self, name):
self.name = name
def eat(self, food):
print('\n{0} is eating {1}'.format(self.name, food))
class Dog(Animal):
def fetch(self, thing):
print('\n{0} goes after the {1}'.format(self.name, thing))
def ShowAffection(self):
print('\n{0} wags its tail'.format(self.name))
class Cat(Animal):
def shred(self):
print('\n{0} shreds the string!'.format(self.name))
def ShowAffection(self):
print('\n{0} purrs'.format(self.name))
# demo code:
def main():
animal_list = [Dog('Rodger'),
Cat('Fluffy'),
Dog('Toby'),
Cat('Felix')]
for animal in animal_list:
animal.ShowAffection()
main()
The 'ShowAffection()' behaviour is polymorphic in the sense that it acts differently depending on the animal (all animals show affection, but they do it differently).
Python itself has many classes that are polymorphic. For example, the 'len()' function can be used with multiple object types and it returns the correct output based on the input parameter:
len("Jupiter") # the type here is 'string'
len([1, 2, 3, 4]) # the type here is 'list'
len(('x', 'y', 3)) # the type here is 'tuple'
Polymorphism allows subclasses to have methods with the same names as methods in their superclasses. It gives the ability for a program to call the correct method depending on the type of object used to call it.
Another example of polymorphism:
# another illustration of polymorphism:
class Animal(object):
def __init__(self, species):
self.__species = species
def show_species(self):
print('\nI am a', self.__species)
def make_sound(self):
print('Grrrrr')
#------------------------------------------------------
class Dog(Animal):
def __init__(self):
Animal.__init__(self, 'Dog')
def make_sound(self):
print('Woof! Woof!')
#-----------------------------------------------------
class Cat(Animal):
def __init__(self):
Animal.__init__(self, 'Cat')
def make_sound(self):
print('Meow')
# test the above classes:
#------------------------------------------------------
def main():
# a function that displays info about animals:
def show_animal_info(creature):
if isinstance(creature, Animal):
creature.show_species()
creature.make_sound()
else:
print('\nThat is not an Animal!')
# instantiate some objects from the above classes:
animal = Animal('regular animal')
dog = Dog()
cat = Cat()
myList = [animal, cat, dog, 'I am a string']
# Display information about each one.
print('Here are some animals and')
print('the sounds they make.')
print('--------------------------')
for item in myList:
show_animal_info(item)
main()
Overriding is the essence of polymorphism. When inheriting from a class, we can alter the behaviour of the original superclass by overriding methods (i.e., by declaring functions/methods in the subclass with the same name, but different implementations). Methods in a subclass take precedence over methods in a superclass.
Here is a very simple example that illustrates this idea:
class Counter(object):
def __init__(self):
self.value = 0
def increment(self):
self.value += 1
def print_current(self):
print('Current counter value: ', self.value)
class CustomCounter(Counter):
def __init__(self, size):
Counter.__init__(self)
self.stepsize = size
def increment(self):
self.value += self.stepsize # this overrides the superclass method
# print_current() will be inherited
#------------------------------------------------------------------------------------
# demo:
def main():
cc = CustomCounter(4)
cc.print_current() # by default all objects have 'value'=0 (initially)
cc.increment() # calls 'increment()' from the subclass
cc.print_current() # you have incremented the 'value'.....
main()
16.6 Inheritance in mathematical programming¶
Before we take a closer look at how the concepts introduced above can be brought to bear upon more abstract matters related to mathematical functions, we re-iterate the generic implementation of a superclass-sublcass relationship:

As a simple example that illustrates the above, we consider the subclass 'Parabola' that extends the class 'Line'; these classes are supposed to represent mathematical objects corresponding to a straight line and a parabola, as their name suggests. We go even further, and introduce an additional class, 'Cubic', which inherits from 'Parabola' and (implicitly) from the class 'Line', too (this is an example of level inheritance).
import numpy as np
from matplotlib import pyplot as plt
class Line(object):
def __init__(self, c0, c1):
self.c0 = c0
self.c1 = c1
def __call__(self, x):
return self.c0 + self.c1*x
def draw(self, ):
x = np.linspace(-5, 5, 30)
y = self(x)
plt.grid()
plt.plot(x,y,'b')
plt.xlabel('x')
plt.ylabel('y')
plt.show()
#
#
# subclass of 'Line':
class Parabola(Line):
def __init__(self, c0, c1, c2):
Line.__init__(self, c0, c1)
self.c2 = c2
def __call__(self, x):
return Line.__call__(self, x) + self.c2*x**2
#
#
# subclass of 'Parabola'
class Cubic(Parabola):
def __init__(self, c0, c1, c2, c3):
Parabola.__init__(self, c0, c1, c2)
self.c3 = c3
def __call__(self, x):
return Parabola.__call__(self, x) + self.c3*x**3
# note that the subclass does NOT have a plotting method
# (but it will inherit draw() from the superclass)
# demo:
q = Line(1, -2) # instantiate object of type 'Line'
q.draw()
p = Parabola(1, -2, 2) # instantiate object of type 'Parabola'
p.draw()
# we manage to plot the parabola because the parent class
# has an implementation of that method....
r = Cubic(2, 3, -2, 1)
r.draw()
# ... the cubic gets plotted because 'Cubic' inherits from 'Parabola', which
# in turn inherits from 'Line'
16.7 Two important examples¶
We are going to look at two more important mathematical examples that take advantage of the idea of inheritance to describe the behaviour of some functions.
The first example is related to functions with parameters (an aspect that we have visited in the past). The idea is to pack together into a single class the function together with numerical approximations for its first and second derivatives. To this end, we introduce the superclass 'MasterClassDerivs' that implements the central finite difference approximation formulae for the 1st and 2nd derivatives of a generic function. We then introduce the subclass 'FuncA', which essentially contains a simple constructor method that allows us to initialize the parameters in the expression of our function, as well as a __call__ method where we define the actual expression of our function. The function we are going to implement in our class is
$$ f(x) = e^{-bx}\sin(ax) $$
where $a$, $b\in\mathbb{R}$ are parameters that the user has the freedom to choose/change.
# inheritance in mathematical programming
# KEY EXAMPLE 1:
import numpy as np
#----------------------------------------------------------------------
# the superclass:
# (abstract, not meant to be instantiated)
class MasterClassDerivs(object):
def __init__(self, h=1.0E-5):
self.h = h
def __call__(self, x):
pass
# raise NotImplementedError\
# ("__call__ missing in class %s" %self.__class__.__name__)
# approx. for the 1st and 2nd derivatives:
# (using central finite difference formulae)
def df(self, x):
h = self.h
return (self(x+h) - self(x-h))/(2.0*h)
def ddf(self, x):
h = self.h
return (self(x+h) - 2.0*self(x) + self(x-h))/(h*h)
#------------------- EndOfSuperclass -----------------------------
#
# a subclass:
# (implementation of a particular function)
#
class FuncA(MasterClassDerivs):
def __init__(self, a, b):
MasterClassDerivs.__init__(self)
self.a = a
self.b = b
def __call__(self, x):
a, b = self.a, self.b
return np.sin(a*x)*np.exp(-b*x)
# Here we test the subclass:
f1 = FuncA(2, 3) # instantiate an object
# this corresponds to a function with specific
# values for 'a' and 'b'
f1(1.0) # you can use this as a normal function
f1(0.0) # another value
f1.ddf(4.0) # this is f1''(4.0)
# the value of the second derivative at x = 4.0
It is possible to derive a subclass from 'MasterClassDerivs' that contains the actual analytical expressions for the derivatives:
\begin{alignat*}{1} f'(x) &= -e^{-bx}\big[b\sin(ax) - a\cos(ax)\big]\\[0.2cm] f''(x) &= e^{-bx}\big[(b^2-a^2)\sin(ax) - 2ab\cos(ax)\big] \end{alignat*}
# this class implements the EXACT derivatives
# (based on the above formulae)
class FuncB(MasterClassDerivs):
def __init__(self, a, b):
MasterClassDerivs.__init__(self)
self.a = a
self.b = b
def __call__(self, x):
a, b = self.a, self.b
return np.sin(a*x)*np.exp(-b*x)
def df(self, x):
a, b = self.a, self.b
t1 = b*np.sin(a*x)
t2 = a*np.cos(a*x)
t3 = -np.exp(-b*x)
res = t3*(t1-t2)
return res
def ddf(self, x):
a, b = self.a, self.b
t1 = (b**2-a**2)*np.sin(a*x)
t2 = 2.0*a*b*np.cos(a*x)
t3 = np.exp(-b*x)
res = t3*(t1-t2)
return res
# demo for the above class
# (exact formulae for the derivative)
f2 = FuncB(2, 3) # instantiate an object
print('Exact value for 2nd derivative at 0.5: {:>20.10f}'.format(f2.ddf(0.5)))
print('Numerical approx for 2nd derivative at 0.5: {:>15.10f} '.format(f1.ddf(0.5)))
The second example is related to Taylor series and their use in constructing approximation for transcendental functions like $\sinh$, $\cosh$, $\sin$, $\cos$, etc.
# inheritance in mathematical programming
# KEY EXAMPLE 2:
from math import factorial
import numpy as np
class Taylor(object):
"""
Abstract class that implements a Taylor polynomial
"""
def __init__(self, N=10):
self.N = N
def __call__(self):
raise NotImplementedError()
def compute(self, x):
sum = 0.0
for i in range(0, self.N):
sum += self(x, i)
return sum
# we use the above abstract class to implement an approximation
# for the hyperbolic cosine function (COSH)
class Cosh(Taylor):
"""
Derived class used for calculating a truncated Taylor polynomial
for the COSH function
"""
def __init__(self):
Taylor.__init__(self)
def __call__(self, x, k):
return (x**(2*k))/float(factorial(2*k))
# demo:
cosh = Cosh() # this is YOUR 'cosh()' -- in Python you
# would need either 'math.cosh' or 'np.cosh'
print('\n x Numerical Exact')
print('----------------------------------------------')
for x in [0.5*k for k in range(1,6)]:
print('{:2.2f} {:5.12f} {:5.12f}'.format(x, cosh.compute(x), np.cosh(x)))

The recommended textbook has a very good discussion of all the basic aspects of OOP. You are expected to supplement the information in these brief notes with some additional reading from the textbook (Chapter 11 is all about 'inheritance' and 'polymorphism').
REFERENCE:
T. Gaddis, Starting out with Python (Fourth Edition), Pearson Education Ltd., 2018